最強の数学勉強法とは？東大受験生もやっているおすすめの勉強法を紹介

「数学の成績が上がらない…」「数学にはセンスが必要？」
数学が苦手な大学受験生は、このような悩みを抱えていませんか？

数学の勉強法で最も大切なのは、問題の「解法パターン」を解明していくことです。

個々の問題に適した解き方を覚えるのではなく、問題の解法に至るまでの思考プロセスや、解法の原理となる抽象化した型を理解することが重要です。

この抽象化した「解法パターン」を理解すると、初見の問題でも柔軟に対応できるようになります。

この記事では、河野塾塾長・河野玄斗が伝授する「最強の数学勉強法」を、具体的な学習ステップと合わせてわかりやすく解説します。

• 数学、英語講師
• 東京大学医学部卒｜三大国家資格制覇（医師&弁護士&公認会計士)

東京大学理科三類に現役合格し、在籍中に司法試験、医師国家試験に短期間の学習で一発合格。テレビ番組『頭脳王』二連覇。公認会計士試験に合格したことでトリプルライセンサーに。 他にも、英検1級、数検1級など数多くの難関試験に合格しており「いかに試験に受かるか」を熟知。YouTubeでの「点数が取れる授業」が人気を博し、受講者は約100万人を超える。

最強の数学の勉強法は「解法パターン」を学ぶこと

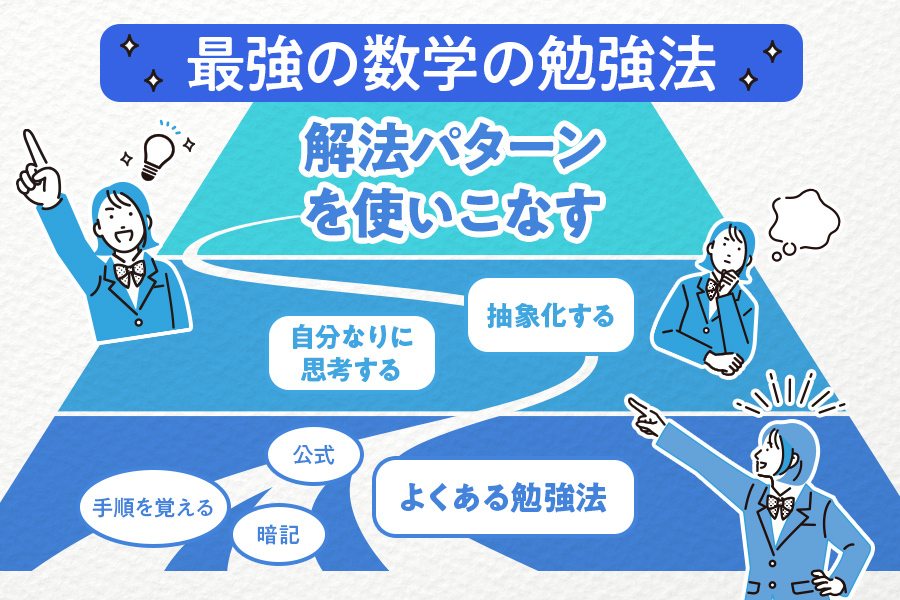
受験数学を攻略するには、再現性がある問題の解法パターンを押さえるのが重要です。

問題を解く際は、解き方だけでなく一歩引いた抽象的な思考プロセス（抽象論）を意識して解法パターンを学習することが、応用問題にも対応できる力に繋がります。

解けなかった問題に直面した際は、問題を解くための解法パターンを洗い出し、論理的にパターンを選んでいく思考法が大切です。「なぜこの問題を解くために、この考え方を使っているのか」と、自分の力で思考していくことを習慣にしていきましょう。

こうした解法パターンを習得するには、数学の基本的な知識や計算力といった基礎学力も必要です。数学の基礎が応用問題の見通しを良くし、解くためのステップ数を減らすことにも繋がります。

抽象論を常に意識し、難易度問わず出会った問題すべてから解法パターンの抽象論を磨き続けることが、応用問題攻略の基礎になります。ぜひチャレンジしてみてください。

では、「解法パターンを学ぶ」とはどういうことか、具体的に解説しましょう。問題を解く時に、次のような流れをイメージしてください。

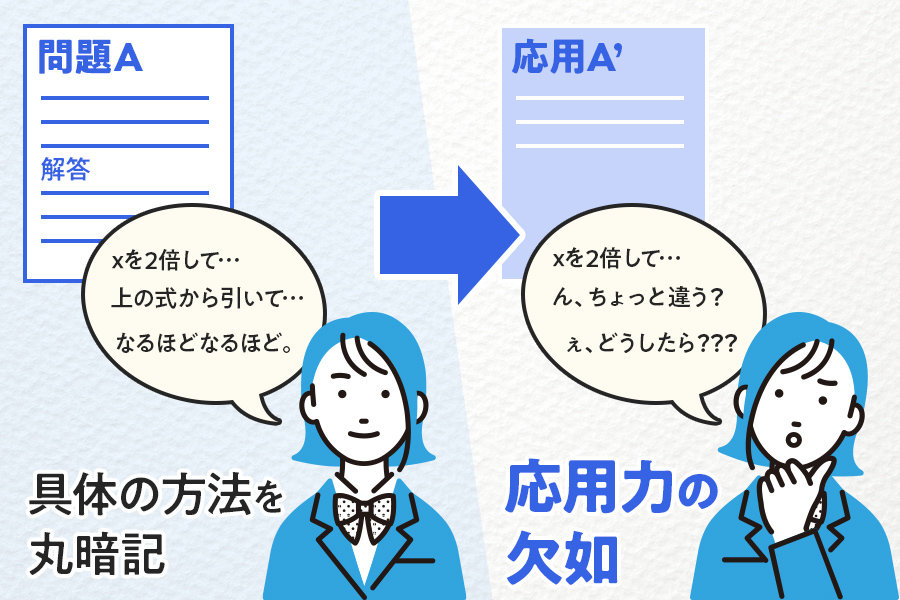
数学の問題Aを演習しているとします。
「この問題の解く手順を覚えよう」と、問題の解き方だけを暗記するのは初学者までです。

この勉強方法では、問題Aに対して適用される解き方だけを学ぶため、応用問題や初見の問題には適用できない可能性があります。

大切なのは、問題Aの解き方だけを覚えるのではなく、その問題を一歩引いた抽象的な思考プロセス（抽象論）を意識して解法パターンを学習することです。

「なぜ問題Aは、このパターンで解けるのか？」と何度も思考を繰り返しましょう。

この思考したプロセスが学びになり、解法に導く抽象化した型、つまり解法パターンを解明していくことに繋がります。

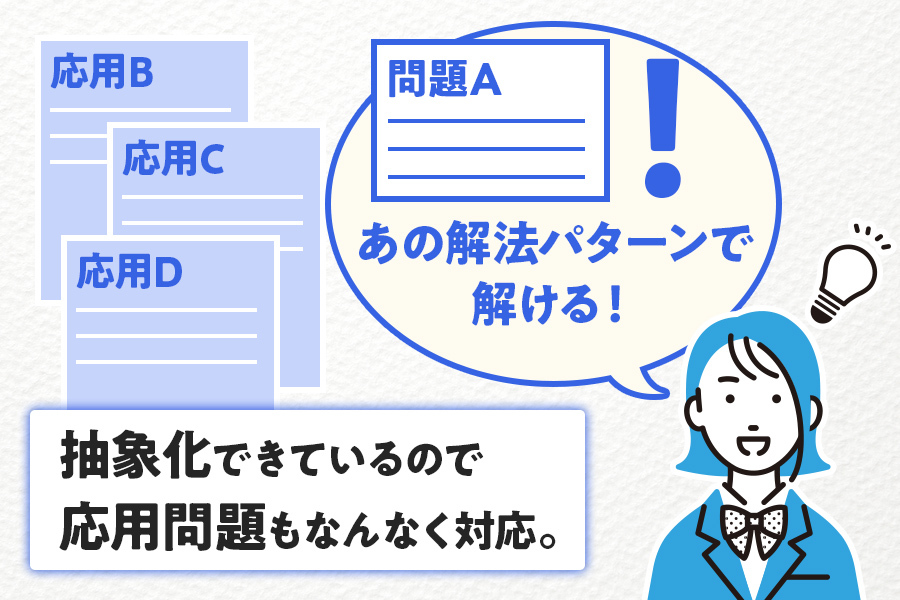
一見異なるように見える問題でも、共通の解法パターンを見つけ出せると、他の応用問題に当てはめて解けるようになります。問題Aだけでなく、応用問題B、C、Dも柔軟に対応できるでしょう。

実例から学ぶ最強の「数学の勉強法」

河野塾チャンネルの動画では、「解法パターン」や「思考プロセス」について具体的に解説をしています。

数学の連立方程式の問題を例に、数学が得意になる思考法を紹介しているので、ぜひチェックしてみてください。

解法パターンを学ぶ勉強法と陥りがちな勉強法の違い

多くの受験生が陥りがちな数学の勉強法と、河野塾が推奨する「解法パターン」を学ぶ勉強法の違いは、次のとおりです。

	解法パターンを学ぶ勉強法	よくある勉強法
学習内容	・解法の抽象化したパターンを知る ・思考のプロセスを学ぶ など	・具体的な問題の解法手順 ・問題の解き方を暗記する など
特徴	「なぜそうなるか」という本質を理解できる	表面的な理解にとどまりやすい
目的	解法の背景にある思考プロセスを理解・再現する	特定の問題の解き方だけを覚える
効果	・初見の問題が解ける ・応用問題にも対応できる	・似た問題しか解けない ・応用が利かない
再現性	高い	低い

「解法パターン」を学ぶ勉強法は、解法の背後にある思考プロセスや本質を理解することで、初見や応用問題にも対応できる「再現性の高い」学習法といえます。

解法パターンを学ぶ3つのメリット

数学の勉強法として「解法パターン」を学ぶことで得られる3つのメリットを紹介します。

メリット1. 数学の苦手意識を克服できる

「自分には数学のセンスがないから無理！」と、苦手意識を持っている受験生は多いと思います。しかし、解法パターンを使うことで最初は難しく見える数学の応用問題でも、次第に解けるようになります。

問題が解けた時、「難しい問題でも自分が知っているパターンを組み合わせれば解けるんだ！」と自信が生まれ、前向きに勉強を進められるようになるでしょう。

この「自分にも解ける！」という成功体験が積み重なることで、数学に対する苦手意識が自然と薄れていきます。

メリット2. 初見の問題でも素早く解答できる

受験数学はある程度の解法パターンが決まっていて、解法までの思考プロセスを学ぶことで、初見の問題にも自信を持って対応できるようになります。

具体的な解法から、一歩引いた抽象的な解法パターンまで理解すれば、様々な応用問題にも対応可能です。

これにより、応用問題の見通しが良くなり、解答までのステップが減るため、素早く解答できるようになります。

メリット3. 難解な問題でも柔軟に解けるようになる

数学の問題は、基本的な問題の組み合わせでできていることがほとんどです。例えば、難しい応用問題を解く過程で、二次方程式を解く場面が出てきたとします。

このとき、二次方程式の解き方（因数分解、解の公式など）が瞬時に出てこないと、応用問題全体を解くのに時間がかかり途中でつまずく原因になります。

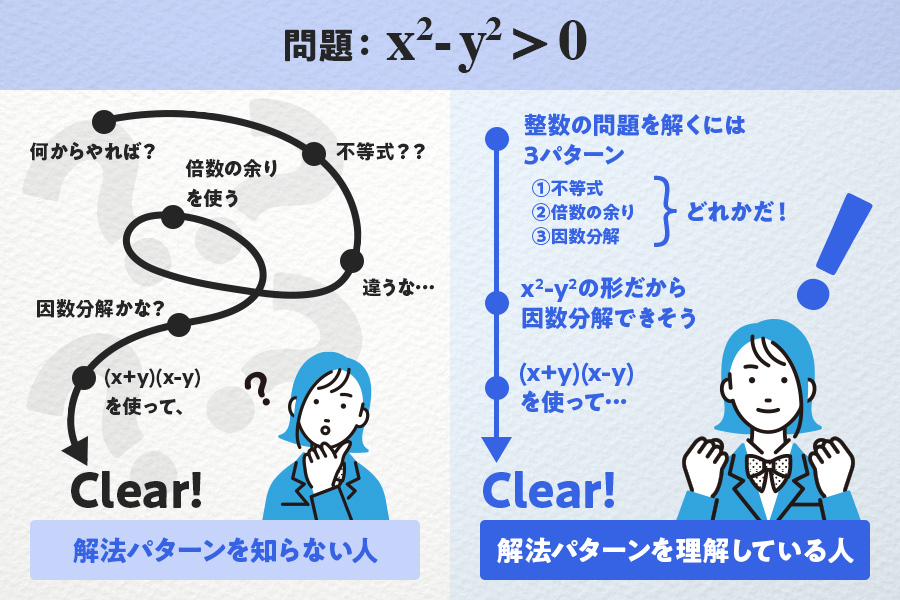
基本的な問題の解法パターンを完璧に身につけ、計算力を高めることで、応用問題を解く際のステップ数を実質的に減らすことができます。

その結果、複雑な問題に対しても、柔軟に解答できるようになるでしょう。

数学の勉強法で失敗するパターン

この章では、数学の勉強法でよく見られる失敗パターンを紹介します。

1. すぐに解答を見る

数学の勉強で問題が解けなかった場合、考えるのを諦めてすぐに解答を見てしまうことがあります。これは、よくある勉強法の失敗パターンです。

一見、効率的な勉強法だと思うかもしれませんが、これは答えを見て「わかったつもり」になるだけで、自分で考える大切なプロセスを省略しています。

数学で重要なのは、試行錯誤して解法を導き出す思考力です。すぐに解答を見てしまうと、考える力が養われず、知識が定着しにくくなります。また応用力も身につきません。

たとえば、大学の過去問を解く際には思いつく解法パターンを全て試してみましょう。成績アップのためには、まず自力で粘り強く考える習慣を身につけることが大切です。

2. 勉強の量だけが目的になる

勉強時間や解いた問題の「量」だけを目標にしてしまうのも、陥りやすい失敗パターンといえます。

ある程度の勉強量は必要ですが「勉強の質」も重要です。学習内容の理解度や、定着度が伴わなければ時間をかけても成績は上がりません。

ただ問題を解き進めるだけの作業になり、間違えた問題の原因分析をおろそかにすると、知識は身につかず思考力も伸び悩んでしまいます。

「長時間勉強をした」「問題集を1周した」ことで満足せずに、「どれだけ理解できたか」「問題を解けるようになったか」という、勉強の質も常に意識することが成績アップには不可欠です。

3. 解けなかった問題を放置する

高校数学の勉強で、解けなかった問題をそのまま放置してしまうケースは、よくあるパターンです。致命的な失敗パターンでもあるので気をつけましょう。

解けなかった問題は、自分の理解が足りていない箇所です。また、弱点や伸びしろを具体的に示してくれる貴重なサインでもあります。

それを放置するということは、自分の苦手分野や、知識の足りない部分をそのままにしている状態です。

「この問題はなぜ解けなかったのか」と原因を分析し、解説書などを読んで理解し、自力で解き直せるようになるまで取り組むようにしましょう。ただし、数字の暗記にならないように注意してください。

こうした解き直しのプロセスこそ、学力を確実に向上させる最大のチャンスです。放置せずに一つずつ弱点を潰していくことが、成績アップへの近道になります。

4. 公式を丸暗記するだけ

勉強を始めた頃は公式の暗記も大切ですが、暗記をしただけでは成績が伸び悩むことがあります。

公式は正しく覚えたうえで、公式の使い方が重要になります。どの問題でどういう場面で使うかを理解するようにしましょう。

公式を適切に使うには、公式の意味や、なぜその答えになるのかを理解し「解法の道具」として使いこなすのが理想です。

覚えた公式は、問題の解法パターンと一緒に使うことで効果を発揮します。公式は問題を解くひとつの道具として考えるようにしましょう。

5. 完璧主義になってしまう

数学の受験勉強において、完璧主義になることは非効率を招きやすいため、おすすめできません。

一つの難問や特定の解法に対して、完璧な理解にこだわりすぎると、そこに膨大な時間を費やしてしまいます。その結果、他の重要な分野の学習や、基礎・標準問題の十分な演習量が確保できなくなる可能性があります。

数学の受験では、戦略的な視点を持つことが重要です。全分野の基本を押さえ、解ける問題は確実に点を取って合格ラインを超えるように勉強を進めていきましょう。

また、試験は時間との戦いでもあります。完璧を目指すあまり、解けるはずの問題に時間をかけられなかったり、難問に時間を使いすぎて全体の得点を落としてしまうため、注意が必要です。

「最強の数学勉強法」は河野塾の徹底基礎講座で学ぼう！

河野塾の徹底基礎講座は、これまで紹介した「解法パターン」と「思考プロセス」をじっくり学べるオンライン講座です。数学力がゼロの人でも、全ての大学入試に対応できるレベルになるように作られています。

数学の徹底基礎講座の特長は、主に4つあります。

1. 本質的な理解を促す解説
   徹底基礎講座では、解き方のみを教えるのではなく「なぜその解法を使うのか？」「どう考えればその発想に至るのか？」という思考プロセスを、講師の河野玄斗がしっかりと言語化して解説をしています。
2. 圧倒的な演習量
   徹底基礎講座で学んだ「解法パターン」と「思考プロセス」を定着させるために、膨大な量の演習問題を用意しています。勉強の質と合わせて量も担保することで、問題を解く力も同時に身につけていきます。
3. 基礎から学べる
   徹底基礎講座は、基本的な問題から徐々に応用問題へステップアップする構成で作られています。数学が苦手な人でも、無理なく学習を進めることができます。
4. 計算力の強化
   問題を素早く正確に解くために不可欠な計算力も、講座を通して自然と身につくように工夫されています。

河野塾の徹底基礎講座なら、数学が苦手な人でも初見の問題や応用問題に対応できる力が身につきます。

徹底基礎講座「数学」を受講した塾生の感想

最後に、河野塾の徹底基礎講座を受講した方の感想をご紹介します。東大受験生も受講した「最強の数学勉強法」の体験談を、ぜひ参考にしてみてください。

受講生Aさんの感想

Q：河野塾の徹底基礎講座を始めたきっかけは？

Q：受講前と受講後で、成績にどのような変化がありましたか？

Q：試験はどうでしたか？

受講生Fさんの感想

Q：河野塾の徹底基礎講座を始めたきっかけは？

Q：数学の徹底基礎講座を受講した感想は？

Q：成績の変化は？

受講生Hさんの感想

受講生Tさんの感想

受講生Kさんの感想

河野塾の徹底基礎講座では「お試し講座」を用意しています。講座の一部を無料で閲覧することができるので、ぜひお試しください。